Archive for the ‘Estimation’ Category
On the accuracy of group estimates
Introduction
The essential idea behind group estimation is that an estimate made by a group is likely to be more accurate than one made by an individual in the group. This notion is the basis for the Delphi method and its variants. In this post, I use arguments involving probabilities to gain some insight into the conditions under which group estimates are more accurate than individual ones.
An insight from conditional probability
Let’s begin with a simple group estimation scenario.
Assume we have two individuals of similar skill who have been asked to provide independent estimates of some quantity, say a project task duration. Further, let us assume that each individual has a probability 
Based on the above, the probability that they both make a correct estimate, 
This is a consequence of our assumption that the individual estimates are independent of each other.
Similarly, the probability that they both get it wrong, 
Now we can ask the following question:
What is the probability that both individuals make the correct estimate if we know that they have both made the same estimate?
This can be figured out using Bayes’ Theorem, which in the context of the question can be stated as follows:
In the above equation, 
Similarly, 
Question: Why?
Answer: If both estimators are correct then they must have made the same estimate (i.e. they must both within be an acceptable range of the right answer).
Finally, 
Now lets apply Bayes’ theorem to the following two cases:
- Both individuals are good estimators – i.e. they have a high probability of making a correct estimate. We’ll assume they both have a 90% chance of getting it right (
).
- Both individuals are poor estimators – i.e. they have a low probability of making a correct estimate. We’ll assume they both have a 30% chance of getting it right (
)
Consider the first case. The probability that both estimators get it right given that they make the same estimate is:
Thus we see that the group estimate has a significantly better chance of being right than the individual ones: a probability of 0.9878 as opposed to 0.9.
In the second case, the probability that both get it right is:
The situation is completely reversed: the group estimate has a much smaller chance of being right than an individual estimate!
In summary: estimates provided by a group consisting of individuals of similar ability working independently are more likely to be right (compared to individual estimates) if the group consists of competent estimators and more likely to be wrong (compared to individual estimates) if the group consists of poor estimators.
Assumptions and complications
I have made a number of simplifying assumptions in the above argument. I discuss these below with some commentary.
- The main assumption is that individuals work independently. This assumption is not valid for many situations. For example, project estimates are often made by a group of people working together. Although one can’t work out what will happen in such situations using the arguments of the previous section, it is reasonable to assume that given the right conditions, estimators will use their collective knowledge to work collaboratively. Other things being equal, such collaboration would lead a group of skilled estimators to reinforce each others’ estimates (which are likely to be quite similar) whereas less skilled ones may spend time arguing over their (possibly different and incorrect) guesses. Based on this, it seems reasonable to conjecture that groups consisting of good estimators will tend to make even better estimates than they would individually whereas those consisting of poor estimators have a significant chance of making worse ones.
- Another assumption is that an estimate is either good or bad. In reality there is a range that is neither good nor bad, but may be acceptable.
- Yet another assumption is that an estimator’s ability can be accurately quantified using a single numerical probability. This is fine providing the number actually represents the person’s estimation ability for the situation at hand. However, typically such probabilities are evaluated on the basis of past estimates. The problem is, every situation is unique and history may not be a good guide to the situation at hand. The best way to address this is to involve people with diverse experience in the estimation exercise. This will almost often lead to a significant spread of estimates which may then have to be refined by debate and negotiation.
Real-life estimation situations have a number of other complications. To begin with, the influence that specific individuals have on the estimation process may vary – a manager who is a poor estimator may, by virtue of his position, have a greater influence than others in a group. This will skew the group estimate by a factor that cannot be estimated. Moreover, strategic behaviour may influence estimates in a myriad other ways. Then there is the groupthink factor as well.
…and I’m sure there are many others.
Finally I should mention that group estimates can depend on the details of the estimation process. For example, research suggests that under certain conditions competition can lead to better estimates than cooperation.
Conclusion
In this post I have attempted to make some general inferences regarding the validity of group estimates based on arguments involving conditional probabilities. The arguments suggest that, all other things being equal, a collective estimate from a bunch of skilled estimators will generally be better than their individual estimates whereas an estimate from a group of less skilled estimators will tend to be worse than their individual estimates. Of course, in real life, there are a host of other factors that can come into play: power, politics and biases being just a few. Though these are often hidden, they can influence group estimates in inestimable ways.
Acknowledgement
Thanks go out to George Gkotsis and Craig Brown for their comments which inspired this post.
The drunkard’s dartboard revisited: yet another Excel-based example of Monte Carlo simulation
(Note: An Excel sheet showing sample calculations and plots discussed in this post can be downloaded here.)
Introduction
Some months ago, I wrote a post explaining the basics of Monte Carlo simulation using the example of a drunkard throwing darts at a board. In that post I assumed that the darts could land anywhere on the dartboard with equal probability. In other words, the hit locations were assumed to be uniformly distributed. In a comment on the piece, George Gkotsis challenged this assumption, arguing that that regardless of the level of inebriation of the thrower, a dart would be more likely to land near the centre of the board than away from it (providing the player is at least moderately skilled). He also suggested using the Normal Distribution to model the spread of hits, with the variance of the distribution serving as a rough measure of the inaccuracy (or drunkenness!) of the drunkard. In George’s words:
I would propose to introduce a ‘skill’ factor, which represents the circle/square ratio (maybe a normal-Gaussian distribution). Of course, this skill factor would be very low (high variance) for a drunken player, but would still take into account the fact that throwing darts into a square is not purely random.
In this post I revisit the drunkard’s dartboard, taking into account George’s suggestions.
Setting the stage
To keep things simple, I’ll make the following assumptions:
Figure 1: The dartboard
- The dartboard is a circle of radius 0.5 units centred at the origin (see Figure 1)
- The chance of a hit is greatest at the centre of the dartboard and falls off as one moves away from it.
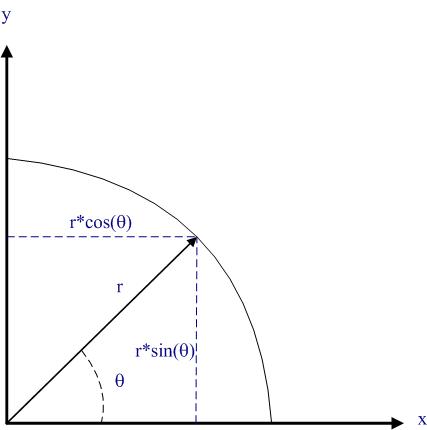
- The distribution of hits is a function of distance from the centre but does not depend on direction. In mathematical terms, for a given distance
from the centre of the dartboard, the dart can land at any angle
with equal probability,
and
coordinates can be obtained using the formulas
and
as s shown in Figure 2.
- Hits are distributed according to the Normal distribution with maximum at the centre of the dartboard.
- The variance of the Normal distribution is a measure of inaccuracy/drunkenness of the drunkard: the more drunk the drunk, the greater the variation in his aim.
Figure 2: The coordinates of a hit location
These assumptions are consistent with George’s suggestions.
The simulation
[Note to the reader: you may want to download the demo before continuing.]
The steps of a simulation run are as follows:
- Generate a number that is normally distributed with a zero mean and a specified standard deviation. This gives the distance,
- Generate a uniformly distributed random number lying between 0 and
. This represents the angle
- The numbers obtained from steps 1 and 2 for completely specify the location of a hit. The location’s
- Re-run steps 1 through 4 as many times as needed. Note that the demo is set up for 5000 runs. You can change this manually or, better yet, automate it. The latter is left as an exercise for you.
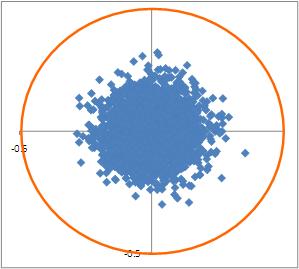
It is instructive to visualize the resulting hits using a scatter plot. Among other things this can tell you, at a glance, if the results make sense. For example, we would expect hits to be symmetrically distributed about the origin because the drunkard’s throws are not biased in any particular direction around the centre). A non-symmetrical distribution is thus an indication that there is an error in the calculations.
Now, any finite collection of hits is unlikely to be perfectly symmetrical because of outliers. Nevertheless, the distributions should be symmetrical on average. To test this, run the demo a few times (hit F9 with the demo open). Notice how the position of outliers and the overall shape of the distribution of points changes randomly from simulation to simulation. In all cases, however, there is a clear maximum at the centre of the dartboard with the probability of a hit falling with distance from the centre.
Figure 3: Scatter plot for standard deviation=0.2
Figure 3 shows the results of simulations for a standard deviation of 0.2. Figures 4 and 5 show the results of simulations for standard deviations of 0.1 and 0.4.
Figure 4: Scatter plot for standard deviation=0.1
Note that the plot has fixed axes- i.e. the area depicted is the 1×1 square that encloses the dartboard, regardless of the standard deviation. Consequently, for larger standard deviations (such as 0.4) many hits will be out of range and will not show up on the plot.
Figure 5: Scatter plot for standard deviation=0.4
Closing remarks
As I have stressed in my previous posts on Monte Carlo simulation, the usefulness of a simulation depends on the choice of an appropriate distribution. If the selected distribution does not reflect reality, neither will the simulation. This is true regardless of whether one is simulating a drunkard’s wayward aim or the duration of project task. You may have noted that the assumption of normally-distributed hits has no justification whatsoever; it is just as arbitrary as my original assumption of uniformity. In fact, the hit locations of drunken dart throws is highly unlikely to be either uniform or Normal. Nevertheless, I hope that some of my readers will find the above example to be of pedagogical value.
Acknowledgement
Thanks to George Gkotsis for his comment which got me thinking about this post.
Uncertainty about uncertainty
Introduction
More often than not, managerial decisions are made on the basis of uncertain information. To lend some rigour to the process of decision making, it is sometimes assumed that uncertainties of interest can be quantified accurately using probabilities. As it turns out, this assumption can be incorrect in many situations because the probabilities themselves can be uncertain. In this post I discuss a couple of ways in which such uncertainty about uncertainty can manifest itself.
The problem of vagueness
In a paper entitled, “Is Probability the Only Coherent Approach to Uncertainty?”, Mark Colyvan made a distinction between two types of uncertainty:
- Uncertainty about some underlying fact. For example, we might be uncertain about the cost of a project – that there will be a cost is a fact, but we are uncertain about what exactly it will be.
- Uncertainty about situations where there is no underlying fact. For example, we might be uncertain about whether customers will be satisfied with the outcome of a project. The problem here is the definition of customer satisfaction. How do we measure it? What about customers who are neither satisfied nor dissatisfied? There is no clear-cut definition of what customer satisfaction actually is.
The first type of uncertainty refers to the lack of knowledge about something that we know exists. This is sometimes referred to as epistemic uncertainty – i.e. uncertainty pertaining to knowledge. Such uncertainty arises from imprecise measurements, changes in the object of interest etc. The key point is that we know for certain that the item of interest has well-defined properties, but we don’t know what they are and hence the uncertainty. Such uncertainty can be quantified accurately using probability.
Vagueness, on the other hand, arises from an imprecise use of language. Specifically, the term refers to the use of criteria that cannot distinguish between borderline cases. Let’s clarify this using the example discussed earlier. A popular way to measure customer satisfaction is through surveys. Such surveys may be able to tell us that customer A is more satisfied than customer B. However, they cannot distinguish between borderline cases because any boundary between satisfied and not satisfied customers is arbitrary. This problem becomes apparent when considering an indifferent customer. How should such a customer be classified – satisfied or not satisfied? Further, what about customers who choose not to respond? It is therefore clear that any numerical probability computed from such data cannot be considered accurate. In other words, the probability itself is uncertain.
Ambiguity in classification
Although the distinction made by Colyvan is important, there is a deeper issue that can afflict uncertainties that appear to be quantifiable at first sight. To understand how this happens, we’ll first need to take a brief look at how probabilities are usually computed.
An operational definition of probability is that it is the ratio of the number of times the event of interest occurs to the total number of events observed. For example, if my manager notes my arrival times at work over 100 days and finds that I arrive before 8:00 am on 62 days then he could infer that the probability my arriving before 8:00 am is 0.62. Since the probability is assumed to equal the frequency of occurrence of the event of interest, this is sometimes called the frequentist interpretation of probability.
The above seems straightforward enough, so you might be asking: where’s the problem?
The problem is that events can generally be classified in several different ways and the computed probability of an event occurring can depend on the way that it is classified. This is called the reference class problem. In a paper entitled, “The Reference Class Problem is Your Problem Too”, Alan Hajek described the reference class problem as follows:
“The reference class problem arises when we want to assign a probability to a proposition (or sentence, or event) X, which may be classified in various ways, yet its probability can change depending on how it is classified.”
Consider the situation I mentioned earlier. My manager’s approach seems reasonable, but there is a problem with it: all days are not the same as far as my arrival times are concerned. For example, it is quite possible that my arrival time is affected by the weather: I may arrive later on rainy days than on sunny ones. So, to get a better estimate my manager should also factor in the weather. He would then end up with two probabilities, one for fine weather and the other for foul. However, that is not all: there are a number of other criteria that could affect my arrival times – for example, my state of health (I may call in sick and not come in to work at all), whether I worked late the previous day etc.
What seemed like a straightforward problem is no longer so because of the uncertainty regarding which reference class is the right one to use.
Before closing this section, I should mention that the reference class problem has implications for many professional disciplines. I have discussed its relevance to project management in my post entitled, “The reference class problem and its implications for project management”.
To conclude
In this post we have looked at a couple of forms of uncertainty about uncertainty that have practical implications for decision makers. In particular, we have seen that probabilities used in managerial decision making can be uncertain because of vague definitions of events and/or ambiguities in their classification. The bottom line for those who use probabilities to support decision-making is to ensure that the criteria used to determine events of interest refer to unambiguous facts that are appropriate to the situation at hand. To sum up: decisions made on the basis of probabilities are only as good as the assumptions that go into them, and the assumptions themselves may be prone to uncertainties such as the ones described in this article.
Eight to Late 